Spel van de week 13 oktober 2020—Egbert Meijer

Het Monty Hall probleem

Monty Hall was een engelse quizmaster uit het verleden die gedurende meer dan dertig jaar een van de eerste televisie spelshows "Let's make a deal" presenteerde. De winnaar mocht aan het eind van de show kiezen uit een van drie deuren waarachter zich een prijs bevond. Tijdens een jubileumshow was de hoofdprijs een auto, mits de deelnemer natuurlijk de juiste deur zou openen. Achter de andere twee deuren bevond zich een geit. De winnaar koos voor deur 2. Alvorens de deur te openen en om de spanning nog wat op te voeren zei de quizmaster 'Let's make a deal'. 'Je hebt voor deur 2 gekozen. Je weet niet zeker of daar de auto achter zit. Zeker is wel dat tenminste achter een van de andere twee deuren een geit staat. Kijk maar, en hij opende deur 3.

U mag nog kiezen voor deur 1 als u dat wilt, of blijft u bij uw eerste keuze? Wat denkt de lezer hiervan, maakt het niet uit en zijn de kansen gelijk of moet de deelnemer nu voor deur 1 kiezen? Dit staat sindsdien in de statistiek bekend als het "Monty Hall problem". Voor wie het probleem nog niet kent, denk er eens over na alvorens verder te lezen.

De bieding gaat:

1SA	2
2	3SA

Wat komt je uit van: Qx xxx QJ109xxx x ?

In een eerder stukje heb ik al verteld dat het vaak goed is om van een korte hoge kleur te starten als de bieding gaat 1SA - 3SA, of zoals hier via Stayman en de leider heeft geen hoge kleur. De 7-kaart Ru heeft geen toekomst. Partner moet een driekaart hebben met de Aas of de Heer, vrijwel uitgesloten na dit biedverloop en sowieso een heel kleine kans. Als we dan toch voor een hoge kleur kiezen dan maar de kleur waarmee we partner het meest helpen, dus Sch Q. Evenwel in een parenwedstrijd zullen de meesten toch voor een veilige Q kiezen, dat geeft in ieder geval geen slag weg.

Nu eerst de oplossing van het drie deuren probleem: je moet onmiddellijk kiezen voor deur 1. Intuitief lijkt het niet uit te maken (fifty-fifty), maar het is wiskundig uit te rekenen dat de kans nu twee keer zo groot is dat de auto achter deur 1 staat. Als de auto achter deur 2 zou zitten had de quizmaster ook deur 1 kunnen openen. Als de auto achter deur 1 zit, moet hij echter deur 3 openen, d.w.z. hij is "beperkt in zijn keuze". Om uw gevoel gerust te stellen: Stel er zijn honderd deuren, waarachter een deur de auto zit. U kiest u favoriete nummer, zeg 43, en de quizmaster opent nu 98 van de resterende deuren om te laten zien dat daar een geit staat. Kiest u nu voor de overgebleven dichte deur of blijft u nog steeds bij uw eerste keuze?

In bridge staat het principe van het Monty Hall probleem bekend als "restricted choice". De speelfiguur kwam voor in spel 12.

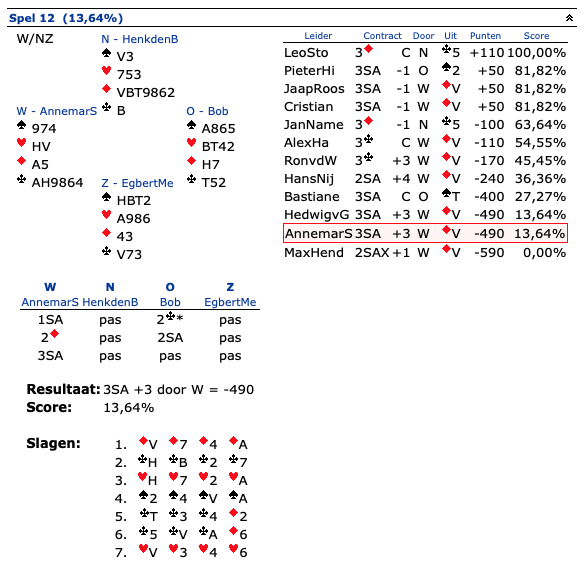
Annemarie opende tegen ons met de West hand 3SA, waarna via Stayman het eindcontract 3SA werd. Na de ruiten start volgde 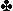A. Noord speelde de B bij. Hoe nu verder? Je kan spelen op het vallen van QJ sec in Noord of snijden op Qxx in Zuid. De kans dat Zuid Q heeft is nu twee keer zo groot als dat Noord die kaart heeft. Net als bij het deurtjes probleem is Noord 'beperkt in zijn keuze', namelijk heeft hij QJ, dan had hij ook de Q kunnen spelen, de Q en J zijn in dit geval gelijk in rang. Als Noord de Q of J singleton heeft, dan moet hij die kaart spelen, hij heeft geen keus. Dat maakt de kans op de Q in Zuid twee keer zo groot. Annemarie gaf Ha Aas nog af en sneed later op Q voor 12 slagen. Mooi gespeeld! Ook Hedwig heeft deze speelwijze gevonden, ik had niet anders verwacht. Anderen die tot 12 slagen kwamen zaten helaas niet in 3SA.

Zoals u ziet had inderdaad de Q lead hier de overslagen tegen gehouden, al had dat voor de score nu niet veel uitgemaakt.